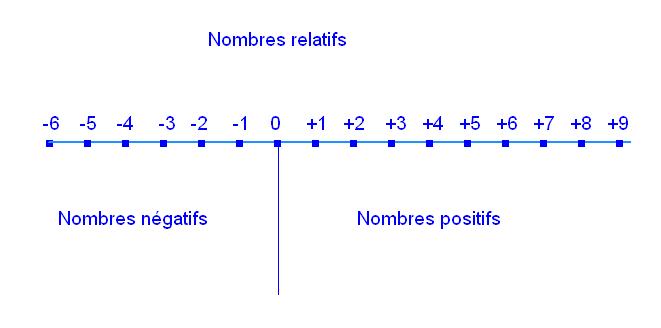
Les nombres relatifs constituent un ensemble étudié au collège, à partir de la 5e. Ils sont identifiables au moyen des signes de calcul qui déterminent leur nature positive ou négative. Découvrez dans cet article comment reconnaître facilement les nombres relatifs et en faire usage dans les opérations mathématiques.
Savoir identifier les nombres relatifs
Par définition, un nombre relatif est un entier naturel muni du signe positif (+) ou du signe négatif (–). Ainsi, les nombres tels que 11, 12, 13, -11, -12, -13 sont tous des entiers relatifs.
Pour mieux illustrer cette notion, prenons l’exemple d’un immeuble de 4 niveaux. Les niveaux situés au-dessus du rez-de-chaussée sont tous affectés d’entiers positifs (niveaux 1, 2 3, 4). Les niveaux situés en dessous du rez-de-chaussée sont tous affectés d’entiers négatifs (niveaux -1, -2, -3, -4). Il faut souligner que tous les entiers naturels sont des entiers relatifs, mais la réciproque n’est pas vraie.
Comment reconnaître un nombre relatif positif ?
Un nombre relatif positif est tout entier supérieur ou égal à 0. Par exemple, 1, 2, 5, 9, 12 sont des entiers relatifs positifs. Pour reconnaître ce type de nombre, il suffit d’observer le signe qui le précède. Si le nombre entier est précédé du signe + ou n’est précédé d’aucun signe, alors il est positif.
Pour une meilleure compréhension, considérons cette opération : 8 ; + 7 ; — 9 + 4 — 6 = 4. Ici, les chiffres positifs sont 8, 7 et 4.
Comment reconnaître un nombre relatif négatif ?
Un nombre relatif négatif est tout entier inférieur ou égal à zéro. Ainsi, -1, -2, -3, -7 et -9 sont des entiers relatifs négatifs. Pour reconnaître un nombre relatif négatif, il faut juste identifier le signe qui le précède. S’il s’agit du signe —, alors il est négatif.
Considérons l’opération suivante : 7 – 4 – 2 + 6 – 3 = 4
On identifie facilement les chiffres négatifs que sont : -4, -2 et -3
Les opérations entre entiers relatifs
Pour effectuer une opération entre ces nombres, il est important de tenir compte de leurs signes. Lorsqu’il s’agit d’une addition de deux entiers de mêmes signes, on écrit leur somme précédée de leur signe commun.
Exemple : 2 + 2 = 4 ; -2 — 1 = – 3
En revanche, s’il s’agit de deux entiers de signes contraires, on écrit le signe du nombre le plus grand. Ensuite, l’on opère la différence du plus grand et du plus petit :
Exemple : – 6 + 2 = – 4 ; 7 — 5 = 2
Afin d’approfondir cette notion, n’hésitez pas à résoudre des opérations entre différents entiers relatifs !